Chirality of Twistane

Molecules which are identical (superimposable) with their mirror image geometries are always optically inactive (achiral); whereas the non-superimposability of a structure with its mirror image results in chirality (optical activity, see below). A simple, but not always accurate test whether a molecule is achiral or not is the presence of a mirror plane (equal to a plane of reflection or plane of symmetry, symmetry element s) in the structure of a molecule. Compounds possessing mirror symmetry are always optically inactive, such as, for example, cis- and trans-1,4-disubstituted cyclohexane derivatives, or symmetrically cis-1,2-disubstituted cyclohexanes (see also the 3D structures at 'Cycloalkanes').

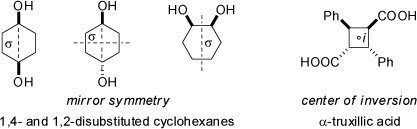In addition, compounds which posses a center of inversion (equal to a center of symmetry, symmetry element i) are also always achiral (see the above example of α-truxillic acid which is of C_i symmetry, but does not have a mirror plane of symmetry).

However, there are molecules featuring neither a mirror plane s nor a center of inversion i, but which are still achiral. Most accurately, all molecules which have a n-fold alternating axis of symmetry (equal to an improper rotation axis or a rotary-reflection axis, symmetry element S_n) are achiral (and thus superimposable with their mirror images). A S_n axis is composed of two successive transformations, first a rotation through 360°/n, followed by a reflection through a plane perpendicular to that axis; neither operation alone (rotation or reflection) is a valid symmetry operation for these molecules, but only the combination of both. Note, that a S₁ axis is identical to a simple mirror plane s, and a S₂ axis is equivalent to a center of inversion i.

Molecules which do not posses a mirror plane s or a center of inversion i, but a S₄ axis are not very common, the examples given below are 1,3,5,7-tetrabromo-2,4,6,8-tetramethyl-cyclooctane and 2,3,7,8-tetramethyl-spiro[4.4]nonane (both S₄ symmetry only). Combinations of S₄ axis with other symmetry elements are common, e.g. methane CH₄ possess three S₄ axis along with six mirror planes s, four C₃ and three C₂ axis; in total the over-all symmetry of methane is described by the T_d point group.

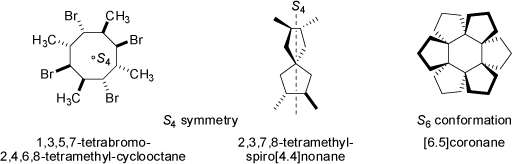On some rare occasions molecules possessing S_n axis with n > 4 are found, the one example above is provided by [6.5]coronane (low-energy solid-state conformation of point group S₆) which also has the symmetry elements i and C₃.

NOTE: In many cases the modern drawings of chemical formulas may erroneously suggest a compound to be of different (i.e. wrong) symmetry than it really is. In all cases, the actually prevailing geometry (very often, but not necessarily the low-energy conformation) of a molecule must be considered when establishing the symmetry of a molecule. Below examples are given, in which chirality results from conformational effects, whereas chemical formulas at first sight suggest planar conformations of molecules (see 'Helical Chirality' below). Chemical formulas are very often helpful, but not always accurate. For example, the above formula of [6.5]coronane virtually implies a D_3d point group (symmetry elements i, three mirror planes s, one C₃, three C₂, and one S₆ axis), but the solid-state conformation actually is of S₆ symmetry (still achiral) only.

The ultimate criterion for chirality (handedness) of a molecule is the non-superimposability of a structure with its mirror image geometry through pure translation and/or rotation only. Chiral molecules related to each other as mutual mirror images may be separated into two enantiomers (reflection isomers, mirror images) with identical chemical (stability and reactivity in achiral environments) and physical (scalar) properties (melting and boiling point, spectroscopic data, etc.), except for their specific optical rotation (the optical activity of enantiomers is of equal absolute magnitude, but of opposite sign).

Chirality of molecules may originate from configurational or conformational effects of structures. This differentiation of configurational and conformational stereoisomers is not allways unambiguous, but generally conformational isomers may interconvert in each other through rotations about C-C single bonds only (this will not interconvert configurational isomers). Below, numerous examples for the different origins of chirality of organic compounds are given.

The formal maxmimum number of configurational stereoisomers (including E/Z-isomers for double bonds) of any compound may be calculated from the number of stereocenters (see 'Asymmetric Substituted Atoms' below) and the number of stereogenic double bonds (double bonds carrying different substitutents at either end, E/Z-isomerism) present in the molecule:

Maxmimum number of configurational stereoisomers: N_max = 2^{(n + m)}

where n = the number of stereocenters and m = the number of stereogenic double bonds.

This includes E/Z-isomers of alkenes which may be regared as configurational isomers (not interconvertible through rotation about C-C single bonds), and which are not superimposable to each other. These isomers are not related to each other as mirror images, and thus they are in fact diastereomers (see also below 'Two or More Asymmetric Substituted Atoms'). For each stereocenter and stereogenic double bond present in a molecule a pair of stereoisomers may be generated (enantiomers or diastereomers).

The actual number of different stereocenter may be smaller than the formal maximum number N_max as defined above if constitutional symmetry is present in the molecule (see below 'Two or More Asymmetric Substituted Atoms' for meso-compounds). Steric strain and geometrical limitations may also reduce the number of possible stereoisomers (e.g. double bonds in small and normal rings may only adopt Z-configuration, or bridged and bicyclic ring systems may require certain rigid linkage geometries and relative configurations of stereocenters - see also below for 'Substituted Adamantane Derivatives').

On the other hand, this maximum number may be exceeded if hindered rotation about C-C single bonds results in additional stereoisomers (see below 'Biphenyls and Binaphthyls').

Any molecule with a single chirality center (any atom holding a set of ligands in a spatial arrangement which is not superimposable on its mirror image) must be chiral. This is the generalized extension of the traditional concept of the asymmetrically substituted carbon atom (van't Hoff): any tetrahedral carbon atom that is attached to four different entities (atoms or groups, e.g. 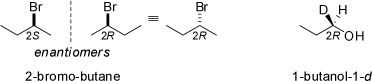CR¹R²R³R⁴) acts as a chirality center, and the corresponding compound may be separated into enantiomers. Thus 2-bromo-butane is chiral (four different substituents -Br, -C₂H₅, -CH₃, and -H at C-2). This rule applies no matter how slight the differences between the four groups are, including isotopic substitution: 1-butanol-1-d is also a chiral compound.

The above defintion is not only restricted to tetrahedral carbon atoms, but to any other type of central atom with an appropriate set of bound groups or ligands. Numerous sulfur derivatives exhibit pyramidal bonding where the non-bonded electron pair located at the sulfur atom acts as a fourth ligand. In many cases these compounds are configurationally sufficiently stable to be separated into enantiomers.

The same would apply to nitrogen derivatives (tertiary amines), but usually these compounds rapidly interconvert through an trigonal planar transition state (pyramidal inversion) and thus prevent separation into enantiomers. Ammonia interconverts 2*10¹¹ times per second, and although this process is slower for substituted amines it is still very fast at room temperature. Exceptions are provided by nitrogen atoms in small rings such as aziridines (for which the trigonal planar transition state of inversion builds up strain energy in the ring), or nitrogen bonded to other atoms with non-bonded electron pairs (such as oxygen). Compounds of these types may be resolved into optically pure enantiomers.

Other examples of configurationally stable amines are bicyclic ring systems with nitrogen located at the bridgehead positions. The geometrical restrictions operative in these ring systems may also prevent inversion. As an typical example, Tröger's base has been separated into enantiomers (see above).

Phosphorous inverts less rapid than nitrogen and arsenic still more slowly. The above rules are not only restricted to tetrahedral centers, but also apply to octahedral and other coordination geometries of appropriate substitution, including metal complexes and inorganic structures.

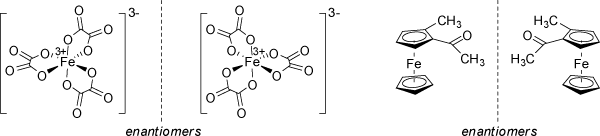The above example of a chiral substituted ferrocene may also be classified as being planar chiral (see below 'Planar Chirality').

Compunds with two or more asymmetrically substituted atoms (chiral centers) may be optically active. Typical examples are (2S,3S)- and (2R,3R)-2,3-dibromo-butane, or (2S,3S)- and (2R,3R)-tartaric acid (german: Weinsäure). However, if pairs of equivalent stereocenters of opposite configuration are present in the molecule, the compounds are optically inactive (achiral meso-compounds) as both chiral centers neutralize each other (internal compensation). For example, (2S,3R)- and (2R,3S)-2,3-dibromo-butane are identical (meso) as both structures can be superimposed through simple rotations and translations only. The same applies to meso-tartaric acid.

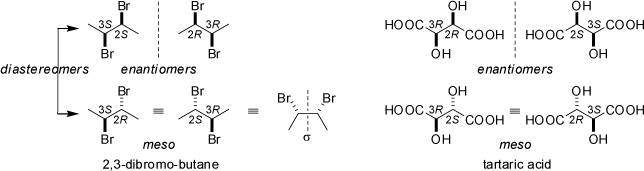Stereoisomers of compunds which are not not related as mirror images are called diastereoisomers. Structures of this type cannot be interconverted into each other through translation, rotation, and mirror symmetry operations. In contrast to enantiomers, diastereoisomers have different chemical (towards achiral as well as chiral reagents) and physical properties (including totally independent values for their specific optical rotation).

trans-1,2-Disubstituted cyclohexanes of C₂ symmetry are chiral compounds, whereas symmetrically cis-1,2-disubstituted cyclohexanes are optically inactive as they posses a mirror plane s of symmetry. However, the latter type compounds exist in chiral conformations which interconvert rapidly into each other through chair-antichair inversions of the cyclohexane ring (see also the 3D structures at 'Achiral Compounds' and the chapter 'Ring Pseudorotation' in the MolArch⁺ - Movies section of this web-site).

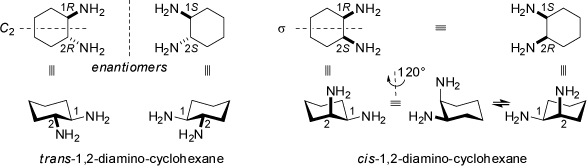Adamantane derivates of suitable substitution may also be chiral compounds. In these structures, not a single atom, but an entire group (the adamantyl residue) holds four substituents (adamantane derivative on the left below) in a spatial arrangement that causes the compound to be non-superimposable with its mirror image geometry. The central adamantyl residue may be regarded as an extended tetrahedron.

This example demonstrates that the stereogenic center of a moleucle needs not to be located on a specific atom. In this case, the stereogenic center is located in the center of the adamantyl cage. Disubstituted adamantanes (note the different substitution positions and pattern) are also chiral compounds - they do not feature a chiral center but an axis of chirality (see below 'Axial Chirality').

In fact, the above (left) adamantane derivative features four asymmetric substituted carbon atoms (the four tertiary carbon atoms of adamantane backbone). As derived above, the formal maximum number of stereoisomers (see abvoe 'Chiral Compounds') would be N_max = 2⁴ = 16. However, in this case only two stereoisomers actually exist, as the steric strain and geometrical limitations of the adamantane resdiue require all substituent to point towards the outside of the molecule (in fact, once the first stereocenter is defined, the remaining three are determined by their relative configuration, and thus the number of observed stereoisomers is 2).

Similar limitations on the number of stereoisomers are observed in almost all bi- and polycyclic systems with small rings. Twistanes (even the unsubstituted parent hydrocarbon) are chiral. As another example, camphor yields two stereoisomers only, although it features two stereocenters in position 1 and 4 (but the relative configuration of both centers is constrained in the bicyclic ring system):

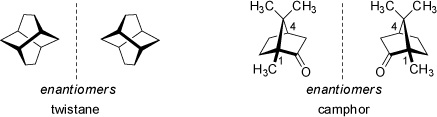Some compounds which do not have asymmetrically substituted carbon atoms (or any other atom type) may still be chiral if they feature two perpendicular planes which are not symmetry planes. If these disymmetric (chiral) planes cannot freely rotate against each other, the corresponding compounds are chiral. Compounds of this type are said to be axially chiral (they feture an axis of chirality instead a center of chirality)

Typical examples are allenes in which the central atom is sp-hybridized, and the planes containing the substitutents on either end of the double bonds are aligned perpendicular to each other (in contrast to simple olefines where all substituents are contained in a single plane of the p-bond; note the difference to E/Z-isomerism of alkenes). For an even number of double bonds in the allene, and if neither side of it is symmetrically substituted, these compounds are optically active and thus chiral.

Very similar arrangements are observed in chiral spiro-annelated ring systems and compounds with exocyclic double-bonds (see examples below).

As demonstrated above, suitably disubstituted adamantane derivatives also show axial chirality (see above 'Substituted Adamantane Derivatives').

The same rules as outlined above for the allenes and spiranes apply also to biphenyl- and binaphtyl-derivatives. If both aromatic ring systems are asymmetrically substituted, the compounds are chiral. As the chirality of these structures originates not from an asymmetrically substituted atom center, but from an asymmetric axis around which rotation is hindered, these enantiomers are also called atropisomers. In the biphenyls, the ortho-substitutents must be large enough to prevent rotation around the central single bond; if hydrogen atoms are present in these positions the barrier of rotation may be too small to prevent interconversion of the enantiomeric forms at room temperature and the two structures may not be separated, or may racemize slowly on standing.

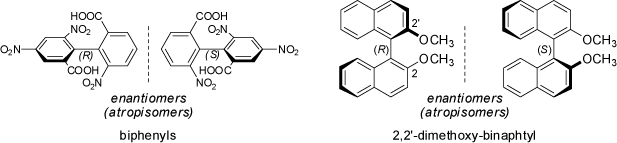Please note, that for the biphenyls and binaphtyls derivatives the formal maximum number of stereoisomers (see above 'Chiral Compounds') is exceeded. As these moleucles do neither feature a stereocenter or a stereogenic double bond, no stereoisomers would be expected. Only the hindered rotation about the central C-C single bond leads to the stereoisomerism of these compounds. Therefore, biphenyl- and binaphtyl-derivatives are conformational stereoisomers (not configurational stereoisomers).

In particular the enentiomerically pure binaphthyl derivatives are of great use in asymmetric catalysis. For some animations of the dynamic behavior of biphenyls and binaphthyls and the process of racemization see the chapter 'Atropsiomers' in the MolArch⁺ - Movies section of this web-site.

Helices are chiral as they can exist in enantiomeric left- or right-handed forms. Typical examples for helical strutures are provided by the helicenes (benzologues of phenanthrene). With four or more rings, steric hinderance at both ends of these molecule prevents the formation of planar conformations, and helicenes rather adopt non-planar, but helical and enantiomeric structures with C₂ symmetry (see also the 3D structures at 'Helicenes' and the chapter 'Racemization of [8]Helicene' in the MolArch⁺ - Movies section of this web-site).

Other examples of chiral helical structures are provided by trans-cyclooctene and suitably substituted heptalenes. Heptalene is not planar, and its twisted structure results in chirality. Although these conformations generally interconvert rapidly, bulky substituents may sufficiently slow down this process to optically resolve and separate these compounds.

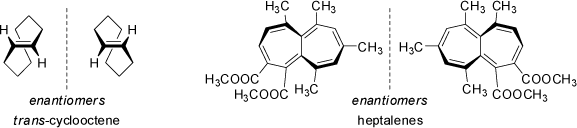The above example of the chirality of (E)-cyclooctene is also example for 'Planar Chirality' (see below).

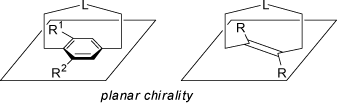
Planar chirality may arise if an appropriately substituted planar group of atoms or ring system is bridged by a linker-chain extending into the space above or below of this plane. Commmon examples are the planar chirality of cyclophanes or alkenes as shown below. Even (E)-cyclooctene is a planar chiral compound (see also above 'Helical Chirality'):

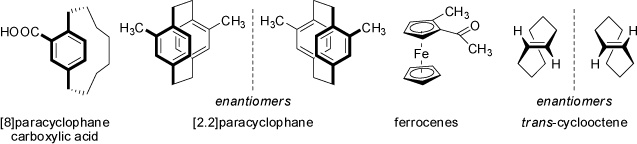The above mentioned suitably substituted ferrocenes are also planar chiral compounds (see 'Asymmetric Substituted Atoms').

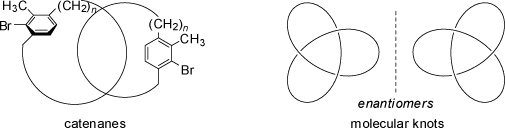
There are many more examples known for which chirality of molecules results from hindered rotation of groups or spatial arrangements of chemical moieties, a few examples are listed below:

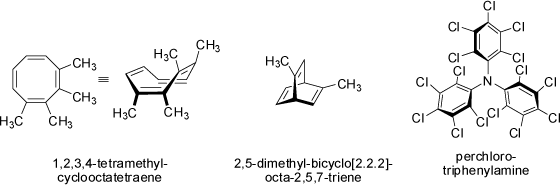Even catenanes and molecular knots made up from achiral molecules are chiral.