PD Dr. Stefan Immel - Hybrid Orbitals

Hybrid Orbitals

Different hybrid orbitals, their formation by mixing various atomic orbitals, and their shapes are discussed here. These hybrid orbitals include the common sp-, sp²-, sp³-orbitals frequently used in organic chemistry, as well as hybrid orbitals including d-functions. The latter are particularly useful for describing the geometries and shapes of transition metal complexes in the field of inorganic chemistry.

Linear Combination of Atomic Orbitals
sp-Hybrid Orbitals
sp-Hybrid Orbitals (Animations)
sp²-Hybrid Orbitals
sp³-Hybrid Orbitals
Hybrid Orbitals with d-Orbitals

All graphics shown on this page were created using the MolArch⁺ program and POVRAY Persistence of Vision Raytracer. Hybrid Orbitals were generated from the pure hydrogenic wave functions of the corresponding atomic orbitals; Cartesian wave functions were taken from The Orbitron Gallery of Atomic Orbitals and Molecular Orbitals. Links are provided for still images as well as to 3D-models (VRML file format, which requires a plugin appropriate for viewing these file type to be installed).

3D-Arrangement of some Hybrid Orbitals

Hybrid Orbitals - Linear Combination of Atomic Orbitals

The Linear Combination of Atomic Orbitals (LCAO) is a mathematical method to construct a new set of orbitals - the hybrid orbitals - by mixing appropriate atomic orbitals (AOs). These hybrid orbitals are useful to account for the "true" geometry of molecules and the directionality of their constituting bonds (e.g. the tetrahedral geometry of methane).

A linear combination of AOs looks like this:

ψ₁

c_1,1

φ₁

c_1,2

φ₂

...

c_1,n

φ_n

ψ₂

c_2,1

φ₁

c_2,2

φ₂

...

c_2,n

φ_n

...

ψ_n

c_n,1

φ₁

c_n,2

φ₂

...

c_n,n

φ_n

Here n atomic orbitals (with their wave functions φ₁, φ₂, ..., φ_n) are used to construct n hybrid orbitals (ψ₁, ψ₂, ..., ψ_n) through a linear combination, where the coefficients c_1,1, c_1,2, ..., c_n,n are normalization constants that must fulfill some requirements:

Hybrid orbitals must be normal:

&sum c_1,n²

c_1,1²

c_1,2²

...

c_1,n²

1.0

and

AOs must be used "completely":

&sum c_n,1²

c_1,1²

c_2,1²

...

c_n,1²

1.0

for all n

An atomic orbital (or hybrid orbital) is normal if the integrals ∫ φ_nφ_n δτ = 1.0 (or ∫ ψ_nψ_n δτ = 1.0 ) - this is the integral over the electron density (which is proportional to φ² or ψ²) over the entire space ( ∫ δτ) must be equal 1.0, or in other words, the probability of finding any electron anywhere in the space must be 100%.

Furthermore, all hybrid orbitals constructed this may must be orthogonal to each other, i.e. the integrals ∫ φ_nφ_m δτ = 0.0 for all n ≠ m - meaning that all possible pairs the newly formed hybrid orbitals must have a zero-overlap in total.

The most common hybrid orbitals in use are the 2sp, 2sp², and 2sp³ orbitals of carbon (used in organic chemistry to the describe the linear arrangement of bonds in alkines, the trigonal-planar geometry in alkenes and the tetrahedral form in alkanes), or the 3sp³d_z² (five AOs yield five hybrid orbitals) and 3sp³d² (six hybrid orbitals) to describe the trigonal-bipyramidal and octahedral geometries of transition metal complexes. Below, examples for the different hybrid orbitals and visualizations of their shapes are given. All orbitals plots on this page are the 90% probability contours of the corresponding electron density (ψ²) with colors indicating opposite signs of the wave function (&psi).

Please note, that hybrid orbitals are a powerful tool to describe the geometry and shape of molecules and metal complexes, yet in "real" molecules their significance may be debated. In "real" cases, someone has to refer more realistically to molecular orbitals instead. This page should give an overview on different geometries of hybrid orbitals, and the consequences for the shape of molecules.

Hybrid Orbitals - 2sp-Orbitals

2sp-Orbitals results from linear combination of a single 2s-orbital with one 2p-orbital (e.g. p_x here; check with conditions for normalization constants above, and note that different colors in the orbital plot correspond to opposite sign of the wave function):

ψ₁ = 1 / √2 φ_2s + 1 / √2 φ_{2p_x} + =

ψ₂ = 1 / √2 φ_2s - 1 / √2 φ_{2p_x} + =

Click the above images to obtain enlarged views of the orbitals, respectively. Please note, that for the sp-orbitals, the common text-book representation places the nucleus at the center between the minor and the major lobe, which in fact is not correct. As obvious from these graphics, the nucleus is embedded in the minor lobe, off the nodal plane of the sp-orbitals.

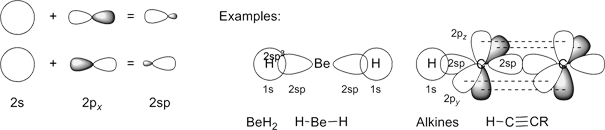Of course, BeH₂ in the solid state is not a monomeric molecule, but forms polymers of the form [BeH₂]_n.

Shapes similar to the 2sp-orbitals (2s + 2p-orbitals) presented here, are found for the 3sp-orbitals and 4sp-orbitals which constructed from 3s + 3p- and 4s + 4p-orbitals, respectively. Yet, as expected the number of nodal planes increases with increasing principal quantum number.

Hybrid Orbitals - 2sp-Orbitals (Animations)

The following links provide some animations on the mixing of a 2s-orbital with a 2p_x-orbital to form the corresponding 2sp-hybrid orbital. All animations are MPEG-movies, and an external player is required (I prefer QuickTime over the Windows Media Player as yields a higher quality, the Media Player suffers from some MPEG-playback artifacts).

Morph of a 2s-orbital into a 2sp-orbital:			→
Morph of a 2p_x-orbital into a 2sp-orbital:			→
Simultaneous transition of a 2s- and 2p_x-orbital into two 2sp-orbitals:			→

Hybrid Orbitals - 2sp²-Orbitals

The linear combination of a 2s-orbital with two 2p-orbitals results in 2sp²-orbitals (e.g. 2s-orbital plus p_x and p_y; check with conditions for normalization constants above, and note that different colors in the orbital plot correspond to opposite sign of the wave function):

ψ₁

1 / √3

φ_2s

1 / √6

φ_{2p_x}

1 / √2

φ_{2p_y}

ψ₂

1 / √3

φ_2s

1 / √6

φ_{2p_x}

1 / √2

φ_{2p_y}

ψ₃

1 / √3

φ_2s

2 / √6

φ_{2p_x}

As for the sp-type hybrid orbitals discussed above, the common text-book representation of sp²-orbitals erroneously places the nucleus at the center between the minor and the major lobe, which is incorrect. As obvious from these graphics, the nucleus is embedded in the minor lobe, off the nodal plane of the sp²-orbitals.

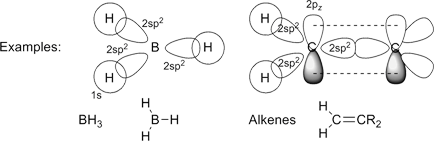Note, that BH₃ usually forms dimers of the type B₂H₆, and may not occur as an isolated molecule.

Similar to the 2sp²-orbitals (2s + 2p_x,y-orbitals), hybrid orbitals can be formed from 3s + 3p_x,y- (3sp²) and 4s + 4p_x,y-orbitals (4sp²).

Hybrid Orbitals - 2sp³-Orbitals

The linear combination of a 2s-orbital with all three 2p-orbitals (p_x, p_y, and p_z) yields four 2sp³-Orbitals (check with conditions for normalization constants above, and note that different colors in the orbital plot correspond to opposite sign of the wave function):

ψ₁

1 / √4

φ_2s

1 / √4

φ_{2p_x}

1 / √4

φ_{2p_y}

1 / √4

φ_{2p_z}

ψ₂

1 / √4

φ_2s

1 / √4

φ_{2p_x}

1 / √4

φ_{2p_y}

1 / √4

φ_{2p_z}

ψ₃

1 / √4

φ_2s

1 / √4

φ_{2p_x}

1 / √4

φ_{2p_y}

1 / √4

φ_{2p_z}

ψ₄

1 / √4

φ_2s

1 / √4

φ_{2p_x}

1 / √4

φ_{2p_y}

1 / √4

φ_{2p_z}

As for the sp-type and sp²-hybrid orbitals discussed above, for the sp³-orbitals the nucleus is embedded in the minor lobe, off the nodal plane.

Similar to the 2sp³-orbitals (2s + 2p_x,y,z-orbitals), hybrid orbitals can be formed from 3s + 3p_x,y,z- (3sp³) and 4s + 4p_x,y,z-orbitals (4sp³).

Hybrid Orbitals with d-Orbitals

Compounds with third row atoms (and above, including transition metals) often involve hybrid orbitals with d-functions. The following table provides an overview on the most commonly used hybrid orbitals with together with the resulting geometrical shapes:

Hybrid Orbitals
Type	Orbitals used	n	Orientation	Shape	Examples
sp	s, p_x	2	linear (digonal)		BeCl₂ (g), CO₂, HCN, HgCl₂, [Cu^I(CN)₂]^- (see above)
sp²	s, p_x,y	3	trigonal-planar		BCl₃ (g), CO₃^2-, NO₃^-, HgI₃^-, CdCl₃^- (see above)
sp³	s, p_x,y,z	4	tetrahedral		BF₄^-, CH₄, NH₄⁺, HgI₄^-, XeO₄ (see above)
sd³	s, d_xy,xz,yz	4	tetrahedral		CrO₄^2-, MnO₄^-
sp²d	s, p_x,y, d_x²-y²	4	square-planar		[Ni^II(CN)₄]^2-, [Pt^IICl₄]^2-
sp³d	s, p_x,y,z, d_x²-y²	5	square-pyramidal		Sb(C₆HC₅)₅, Ni(PR₃)₂Br₃ (rare)
sp³d	s, p_x,y,z, d_z²	5	trigonal-bipyramidal		PF₅, PCl₅, SbCl₅, [Fe⁰(CO)₅]⁰
sp³d²	s, p_x,y,z, d_x²-y²,z²	6	octahedral		SF₆, PF₆^-, SiF₆^2-, XeO₆^4-, [Mn^IIICl₆]^3-, [Fe^III(CN)₆]^3-
sp³d³		7	pentagonal-bipyramidal		IF₇, ZrF₇^3-, UF₇^3-
sp³d⁴		8	square-antiprismatic		TaF₈^3-

See the table below for some examples of transition metal complexes and their geometries. Click the hybrid designations to view images of the corresponding orbitals.

Electron Configuration (Z)

Compound ZL_n