| TUD Organische Chemie | Immel | Tutorials | Symmetry | Examples: Molecules | View or Print (this frame only) |
On this page numerous examples of molecules belonging to different point groups are provided. For a detailed descriptions on the symmetry and properties of point groups (including the corresponding stereographic projections, shapes of objects, list of essential symmetry elements, and a detailed description on how to determine the point group of a given molecule) see the 'Symmetry and Point Groups' section of this web site.
|
|
||||||||||||||||||
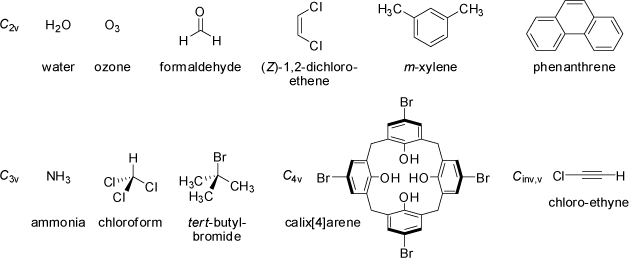
Molecules having a n-fold rotation axis Cn and n vertical mirror planes σv belong to
the Cnv point group. Linear molecules which do not possess an inversion center or a horizontal mirror plane σh
belong to the C∞v point group, because all rotations about their axis are symmetry operations (conical molecules).
|
|||||||||||||||||||
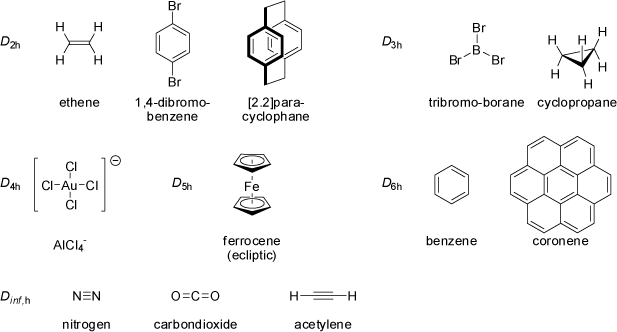
If, in addition to a n-fold principal axis and n twofold axes perpendicular to it, a horizontal mirror plane σh
is present in a molecular structure, the point group is described as Dnh. The D∞h point group includes all linear molecules
with an center of inversion, which also implies a horizontal mirror plane σh (cylindrical molecules).
|
|||||||||||||||||||
The tetrahedral point groups are characterized by the presence of four C3 principal axes (and three C2 axes).
The Td group is the point group of a regular tetrahedron. If, in addition, a center of inversion is present, the point group is Th (molecules
of this group do not look like tetrahedrons, but retain the rotational symmetry of a tetrahedron). All objects possessing the rotational symmetry of a tetrahedron, but no
plane of reflection or center of inversion are based on the simpler point group T. Molecules of this group must be chiral, and examples are very rare.

|
|||||||||||||||||||
The octahedral point groups O and Oh feature three C4 principal axes (and four C3 axes as well as multiple C2 axes).
A regular octahedron and a cube both belong to the Oh point group. In analogy to the tetrahedral point group T, the octahedral group O retains the
rotational symmetry of an regular octahedron, but none of its planes of reflection or the center of inversion. Examples of molecules belonging to the
O point group are extremely rare (these molecules must be chiral!).

|
|||||||||||||||||||
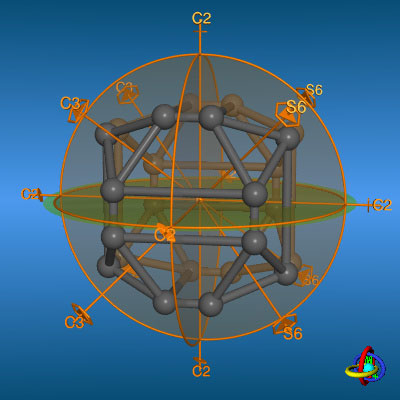
The icosahedral point groups I and Ih posses six C5 principal axes (amongst 10 C3 and 15 C2 axes).
In analogy to the octahedral point groups O and Oh the I group does contain all rotational symmetry elements, but no
mirror planes or center of inversion. Molecules belonging to this chiral point groups are extremely rare. Shapes belonging to the more
symmetrical Ih point groups are the dodecahedron and the icosahedron.

|
|||||||||||||||||||
The Kh point group resembles the symmetry of perfect spheres. Obviously, only atoms but no molecules belong to this point group.
|
|||||||||||||||||||









![2,6,7-Trimethyl-1-aza-bicyclo[2.2.2]octan](symmetry_C3/small_BCYCOCT.jpg)
![Calix[4]arene Derivative](symmetry_C4/small_CALIX04.jpg)






![Calix[4]arene](symmetry_C4v/small_CALIX04.jpg)










![[2.2]Paracyclophane](symmetry_D2h/small_PARAPHAN.jpg)













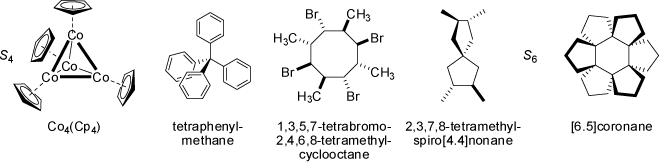


![2,3,7,8-Tetramethyl-spiro[4.4]nonane](symmetry_S4/small_SPIRO44.jpg)
![[6.5]Coronane](symmetry_S6/small_CORONANE.jpg)

![Fe[(C5H5N)6]2+](symmetry_Th/small_FEPYR6.jpg)










![[60]Fullerene (C60)](symmetry_Ih/small_CARBON60.jpg)