TUD Organische ChemieImmelPublicationsPapersAbstract 24View or Print (this frame only)View or Print (this frame only)

Molecular Modeling of Saccharides, Part XXII.

Conformations and Lipophilicity Profiles of Some Cyclic β(1→3)- and β(1→6)-linked Oligogalactofuranosides

Holger Gohlke, Stefan Immel, and Frieder W. Lichtenthaler

Carbohydr. Res., 1999, 321, 96-104.

The conformational features of small cyclogalactins composed of β(1→3)- and β(1→6)-linked galactofuranose units, i.e. cyclo[D-Galf β(1→3)]n with n = 4 (1) and 5 (2), and cyclo[D-Galf β(1→6)]n with n = 3 (3) and 4 (4), were investigated by means of Monte-Carlo simulations. The flexibility of the macrocyclic backbone strongly favors bent and asymmetrical conformations over round geometries. Generation of the molecular surfaces of the global energy-minimum structures reveal disk-type shapes for 1 - 4 without through-going central cavities, yet distinct indentations close to the O-2 / O-3-groups, respectively. The molecular lipophilicity patterns prove these surface dents to be hydrophobic for the β(1→6)-linked cyclogalactins 3 and 4, whereas their β(1→3)-linked counterparts display an inverse situation with a hydrophobic outer core structure.

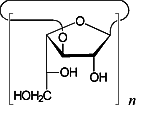beta(1->3)-cyclogalactofuranoside cyclo[D-Galf β(1→3)]n
n = 4,5		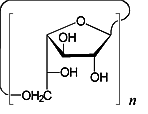 beta(1->6)-cyclogalactofuranoside cyclo[D-Galf β(1→6)]n
n = 3,4

cyclo[D-Gal f beta(1->3)]4 cyclo[D-Gal f beta(1->3)]5 cyclo[D-Gal f beta(1->6)]3 cyclo[D-Gal f beta(1->6)]4
cyclo[D-Galf β(1→3)]4
1		 cyclo[D-Galf β(1→3)]5
2		 cyclo[D-Galf β(1→6)]3
3		 cyclo[D-Galf β(1→6)]4
4
surface of cyclo[D-Gal f beta(1->3)]4 surface of cyclo[D-Gal f beta(1->3)]5 surface of cyclo[D-Gal f beta(1->6)]3 surface of cyclo[D-Gal f beta(1->6)]4
cross-cut of cyclo[D-Gal f beta(1->3)]4 cross-cut of cyclo[D-Gal f beta(1->3)]5 cross-cut of cyclo[D-Gal f beta(1->6)]3 cross-cut of cyclo[D-Gal f beta(1->6)]4
Figure 1: Chemical formulas (top row) and global energy-minimum structures of the cyclogalactofuranosides 1 - 4 with their contact surfaces in dotted form (center). All structures are displayed perpendicular to the macrocycles with the O-2 / O-3 sides facing the viewer. In addition, surface cross-section plots perpendicular to the mean macro-ring planes are shown (bottom row), with approximate molecular dimensions in Å.

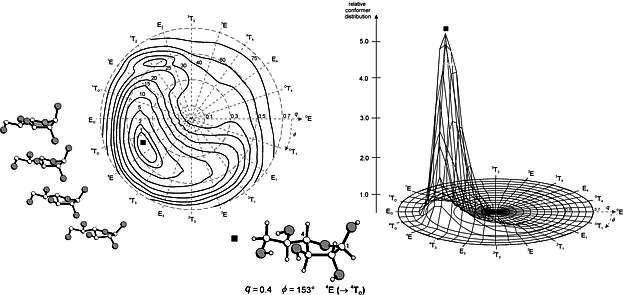
energy potential surface of galactofuranose
Figure 2: Left: Adiabatic energy map of β-D-galactofuranose as a function of the furanose Cremer-Pople parameters - i.e. the puckering amplitude q and the phase angle f - calculated by molecular mechanics using the PIMM91 force-field (energies are given in kJ/mol). The bold-faced square marks the global energy minimum corresponding to the conformation displayed underneath (4E form slightly distorted towards the 4TO geometry); the structures to the left represent the furanose conformations within 4T3<-> EO range of the pseudorotational turntable. Right: 3D-Contour plot of the relative Boltzmann distribution of conformers calculated for T = 300 K, indicating finite conformer probabilities within the 10 kJ/mol contour line.

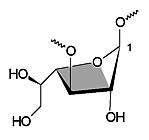
furanose conformation in beta(1->3)-linked cyclogalactins furanose conformation in beta(1->6)-linked cyclogalactins
1E 4T3
Figure 3: Schematic representation of the furanose geometries calculated for cyclogalactofuranosides 1 - 4: 1E conformation for the β(1→3)-linked cyclooligosaccharides 1 and 2 (left) versus the 4T3 form for the β(1→6)-analogs 3 and 4 (right).

Additional Graphics: Cyclogalactins

© Copyright PD Dr. S. Immel